How To Find Acceleration On A Velocity Time Graph

What Is Acceleration

• Rate of change of velocity is chosen acceleration. It is a vector quantity
  \(i.east.\text{    }a=\frac{v-u}{t}\)
  where u is the initial velocity of the object, v is its final velocity and t is the fourth dimension taken.
• Unit of acceleration = one thousand/s^two or ms^-ii
• If the velocity of a body decreases, and then it will experience a negative dispatch which is called deceleration or retardation.
• Figure shows a car moving along a straight line. The speedometer of the auto shows that it is moving with increasing velocity. The auto is accelerating.
  
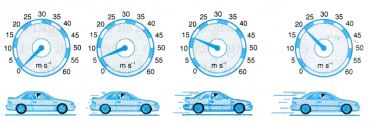
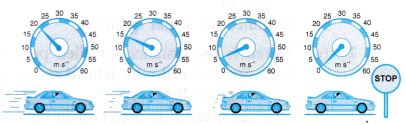
• We say that an object is undergoing a deceleration or retardation when it is slowing down. The rate of change of velocity of the object then has a negative value. Figure shows a car decelerating. The speedometer of the car shows that information technology is moving with decreasing velocity.

Types of acceleration

Uniform acceleration:If a body travels in a straight line and its velocity increases by equal amounts in equal intervals of time then it is said to be in state of uniform acceleration.
e.g. motion of a freely falling body.

Not uniform acceleration:A body has a non-compatible acceleration if its velocity increases by unequal amounts in equal intervals of time.

Instantaneous acceleration: The dispatch of a body at any instant is chosen its instantaneous acceleration.

Dispatch is determined by the gradient of time-velocity graph.
\(\tan \theta =\frac{dv}{dt}\)

1. If the time velocity graph is a straight line, acceleration remains constant.
2. If the slope of the straight line is positive, positive dispatch occurs.
3. If the gradient of the straight line is negative, negative dispatch or retardation occurs.

Analysing Motion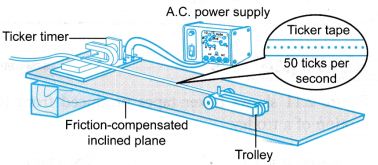

1. Effigy shows a set-upwards of appliance to analyse motion in the laboratory.
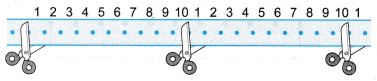
2. (a) A ticker timer is an apparatus that gives a permanent tape of motion for farther analysis. When continued to an alternating current (a.c.) power supply (usually 12 V), it vibrates at a frequency of 50 Hz.
   (b) The ticker timer makes a series of dots at a charge per unit of 50 dots per second on a piece of ticker tape every bit information technology is pulled through the timer by a trolley. Therefore, the time interval of a dot and the adjacent dot which is besides known as one tick is 1/50 or 0.02 s.
   (c) The altitude betwixt two dots is equal to the altitude travelled by the trolley during the time interval between the dots.
   (d) The ticker tape can be analysed to decide the time, displacement, average velocity, acceleration and type of motility of an object.
3. The ticker record can be cut into strips of equal time (equal number of ticks) and pasted together to form a chart for analysing the motion of a trolley.
4. Figure shows three charts formed from strips of ticker record, each consisting of x ticks.
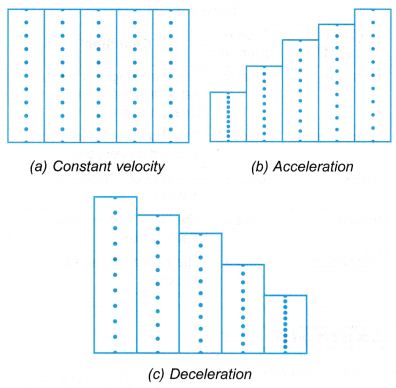
5. For motion with compatible acceleration or deceleration, its value can be determined by analysing the nautical chart. Figure shows a chart formed from strips of ticker tape with ten ticks each.
   
   
   

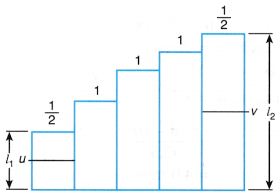
Acceleration Using A Velocity Time Graph Example Problems With Solutions

Example 1. A van accelerates uniformly from a velocity of x m s^-1to 20 m s^-one in ii.5 s. What is the dispatch of the van?
Solution: Initial velocity, u = x ms^-1
Final velocity, v = 20 ms^-1
Time taken, t = ii.v s

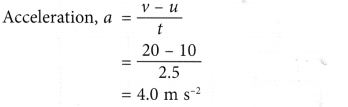
Example 2.A car travelling at 24 thousand s^-1 slowed downwardly when the traffic calorie-free turned cerise. Afterward undergoing uniform deceleration for 4 southward, information technology stopped in front of the traffic light. Calculate the dispatch of the car.
Solution: Initial velocity, u = 24ms^-1
Final velocity, v = 0 ms^-1
Fourth dimension taken, t = 4 s

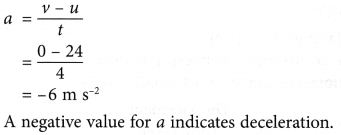
Example 3.Time-velocity graph of a body is shown in the figure. Detect its acceleration in 1000/sⁱⁱ.
Solution:    As information technology is clear from the effigy,
At t = 0 s, v = 20 m/s
At t = 4 s, five = lxxx m/s

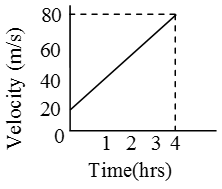
\(therefore \text{Dispatch,}a=\frac{\text{Change}\,\text{in}\,\text{velocity}}{\text{Timeint}\,\text{erval}} \)
\( =\frac{\Delta v}{\Delta t}=\frac{{{v}_{2}}-{{five}_{ane}}}{{{t}_{2}}-{{t}_{1}}} \)
\( =\frac{(80-xx)\,}{(iv-0)}=15\text{ m/}{{\text{s}}^{\text{ii}}} \)

Example 4.Time-velocity graph of a particle is shown in effigy. Notice its instantaneous dispatch at post-obit intervals

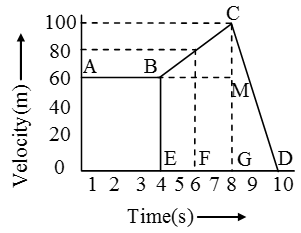
(i) at t = 3s
(ii) at t = 6s
(iii) at t = 9s
Solution: (i) Instantaneous acceleration at t = 3s, is given by
a = slope of line AB = nothing
(ii) Instantaneous dispatch at t = 6 s, is given by a = slope of line BC
\( =\frac{CM}{BM}=\frac{100-60}{8-4}=\text{ }10\text{ m/}{{\text{s}}^{\text{ii}}} \)
(iii) Instantaneous acceleration at t = 9 s, is given past a = slope of line CD
\( =\frac{0-100}{ten-8}=-fifty\text{ thou/}{{\text{s}}^{\text{ii}}} \)

Case 5.Starting from rest, Deepak paddles his bike to accomplish a velocity of vi m/south in 30 seconds then he applies brakes so that the velocity of the bicycle comes down to iv k/s in the next v seconds. Calculate the acceleration of the bicycle in both the cases.
Solution:   (i) Initial velocity, u = 0, final velocity,
v = half-dozen grand/s, fourth dimension, t = thirty s
Using the equation v = u + at, we have
\( a=\frac{five-u}{t} \)
substituting the given values of u, five and t in the above equation, nosotros get
\( a=\frac{half dozen-0}{thirty}=0.ii\text{ grand/}{{\text{s}}^{\text{2}}}\text{; }\!\!~\!\!\text{ } \)
which is positive acceleration.
(ii) Initial velocity, u = 6 m/s, final velocity,
v = iv m/s, fourth dimension, t = 5 south, and then
\( a=\frac{v-u}{t}=\frac{four-6}{5}=-0.four\text{ g/}{{\text{s}}^{\text{2}}}\text{; }\!\!~\!\!\text{ } \)
which is retardation.
Note: The acceleration of the instance (i) is positive and is negative in the case (ii).

Example half dozen. A trolley pulled a ticker record through a ticker timer while moving down an inclined plane. Figure two.10 shows the ticker tape produced.

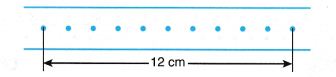
Determine the average velocity of the trolley.
Solution:

Case 7. Figure shows ticker tapes produced from the motion of a trolley.

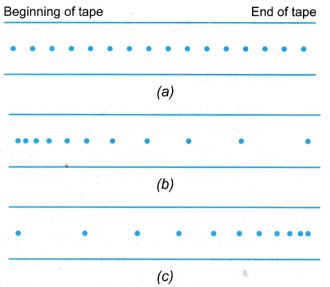
Describe the blazon of motion of the trolley for each ticker tape.
Solution:
(a) The distances between two neighbouring dots are the same throughout the tape. Therefore, the trolley moved with uniform velocity.
(b) The distances betwixt two neighbouring dots are increasing. Therefore, the trolley moved with increasing velocity The trolley was accelerating.
(c) The distances between ii neighbouring dots are decreasing. Therefore, the trolley moved with decreasing velocity. The trolley was decelerating.

Example 8. Effigy shows a chart representing the motion of a trolley with uniform dispatch.

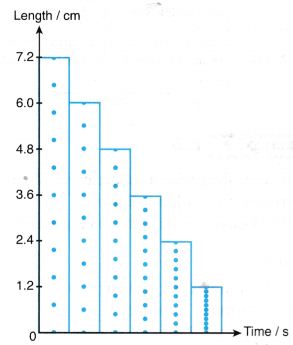
Determine its dispatch.
Solution:

Example 9. A trolley travelled down an inclined aeroplane pulling along a ticker tape. Figure shows a chart formed by cutting and arranging the ticker tape into strips of ten ticks each.

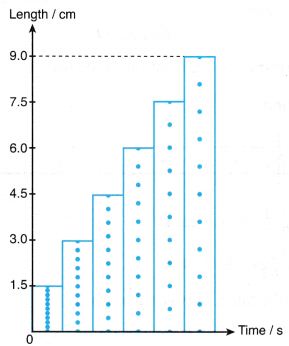
Determine the dispatch of the trolley.
Solution:

Example x. Figure shows a strip of ticker tape depicting the motion of a toy car with uniform dispatch.

Determine the acceleration of the toy car.
Solution:

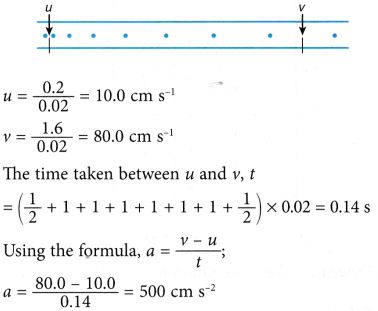
Source: https://www.aplustopper.com/acceleration-and-types-of-acceleration/

Posted by: dennytheept.blogspot.com

Share this post