How To Find The Next Number In A Sequence

Finding the Next Number in a Sequence:
The Method of Mutual Differences (page 1 of 7)

Sections: Common differences, Recursions, General examples, Not-math "sequences"

When faced with a sequence for which you need to detect missing values or the side by side few values, you need first to look at it and see if you tin get a "experience" for what is going on. For case:

Notice the next number in the following sequence: i, 4, 9, xvi, 25, ....

I notice that 1² = ane, ii² = iv, three² = nine, iv^two = sixteen, and 5² = 25 . So it looks as though the blueprint here is squaring. That is, for the offset term (the 1 -st term), it looks like they squared 1 ; for the second term (the 2 -nd term), they squared 2 ; for the third term (the iii -rd term), they squared three ; and then on. For the n -thursday term ("the enn-eth term"), they will probably want me to square n . In particular, for the sixth term, they will probably want me to square 6 .

The side by side number in the sequence is half dozen² = 36 .

Why is the respond only "probably" the square of 6? Because "the correct answer" is zip more than than whatever answer the author had in listen when he designed the exercise; you might "see" a completely different pattern that he hadn't intended. But as long as your reply is something that yous can mathematically (or at least logically) justify, your answer should exist adequate, even if it isn't "correct".

Observe the next number in the following sequence: i, 4, 27, 256,....

This blueprint looks like to the previous sequence, but with 1¹ = ane, two² = 4, threeⁱⁱⁱ = 27, and 4⁴ = 256 . The pattern seems to be that the north -th term is of the class n^{due north} .

Then the next term, being the fifth term (n = 5) is 5⁵ = 3125 .

Find the next number in the following sequence: 2, 5, 10, 17, 26, ....

I take to exist more clever to effigy out the pattern on this sequence. Each term is 1 more than a foursquare. That is, the pattern is given by:

northward	n ²	due north ² + ane
1	i	2
two	4	5
3	9	10
4	sixteen	17
5	25	26

So the n -th term is given by n ² + 1 . And so the sixth term is:

half-dozen^two + 1 = 36 + ane = 37

Annotation that these two sequences were generated by the polynomials n ² and north ⁱⁱ + ane . But what if the sequence is generated by a more than complicated polynomial? How would you lot figure it out then? In that location is a method, and I'll demonstrate it by re-doing the 2nd sequence higher up, where nosotros already know what the blueprint is. Copyright � Elizabeth Stapel 2002-2011 All Rights Reserved

Find the next number in the post-obit sequence: 2, 5, ten, 17, 26, ...., and provide a formula for the n -th term.

To observe the pattern, I volition listing the numbers, and find the differences for each pair of numbers. That is, I will subtract the numbers in pairs (the first from the 2d, the 2nd from the third, and so on), similar this:

Since these values, the "first differences", are non yet value, I'll keep subtracting:

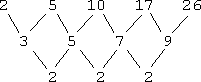
second differences

Since these values, the "second differences", are all the aforementioned value, and so I tin can stop. It isn't important what the second difference is (in this case, "2 "); what is important is that the second differences are the same, because this tells me that the polynomial for this sequence of values is a quadratic. (Once you've studied calculus, you'll exist able to understand why this is so. For now, just trust me that this works.) Since the formula for the terms is a quadratic, then I know that it is of the form:

an ² + bn + c

...for some numbers a , b , and c . At present I accept to find those numbers. How? By plugging in some of the values from the sequence, and so solving the resulting system of equations . For case, I know that the beginning term (that is, the term when due north = 1 ) is 2 , so I'll plug in 1 for n and 2 for the value:

a(1)² + b(1) + c = a + b + c = two

The second term (that is, the term when n = ii ) is 5 , so:

a(ii)^two + b(ii) + c = 4a + twob + c = v

The third term (that is, the term when n = 3 ) is 10 , so:

a(iii)^two + b(three) + c = 9a + threeb + c = x

This gives me a organization of three equations in iii unknowns, which I tin solve. You can use whatever method you like, including using matrices in your graphing calculator:

screen-shot of calculator solution

(Remember that calculators endure from round-off error. When you get a result similar "1.three E �13 ", which represents "0.00000000000013 ", you should be enlightened that, in this context, this means "zero".)

Then a = 1, b = 0 , and c = i , so the formula is:

1n ² + 0n + 1 = n ² + 1

...just as I had adamant before, and the sixth term is:

next term: 6² + 1 = 36 + 1 = 37
formula for the n -thursday term: n ⁱⁱ + i

You lot tin can simplify your computations somewhat by using a formula for the leading coefficient of the sequence's polynomial. The coefficient of the first term of the polynomial will be equal to the common deviation divided by the factorial of the polynomial's caste. In the example higher up, the mutual difference was 2 and the degree was two , and then the leading coefficient was ii � 2! = ii � 2 = 1 . I'm not aware of any formulas for the other coefficients.

Top | 1 | 2 | iii | four | 5 | 6 | seven| Return to Alphabetize Side by side >>

Cite this article every bit:

Stapel, Elizabeth. "Finding the Side by side Number in a Sequence: The Method of Mutual Differences."
Purplemath. Available from https://www.purplemath.com/modules/nextnumb.htm .
Accessed